Micrograd - Autograd Engine for Neural Networks
A tiny auto-differentiation engine and a small neural network from scratch in Python, inspired by Andrej Karpathy's micrograd.
Image Gallery
Click on an image to read more about it.

Computation graph for a three-layer MLP
This is a computation graph produced by Micrograd for a feed-forward neural network with three layers. Each layer consists of neurons with weights and biases and tanh activations.

Smaller computation graph
This is a much smaller computation graph. It is essentially a computation graph for a single (small) layer. It consists of two neurons with two weights and one bias, and a tanh activation function.
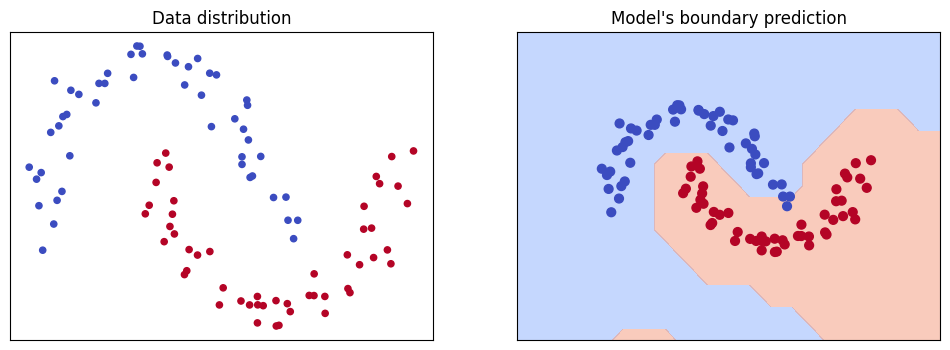
Using Micrograd to predict data distribution
Generating a distribution of data of two sets of points in the shape of two moons, I trained a four-layer Micrograd-powered neural network to predict the boundary between the two sets of points. As you can see, the prediction was quite accurate (>99% accuracy).
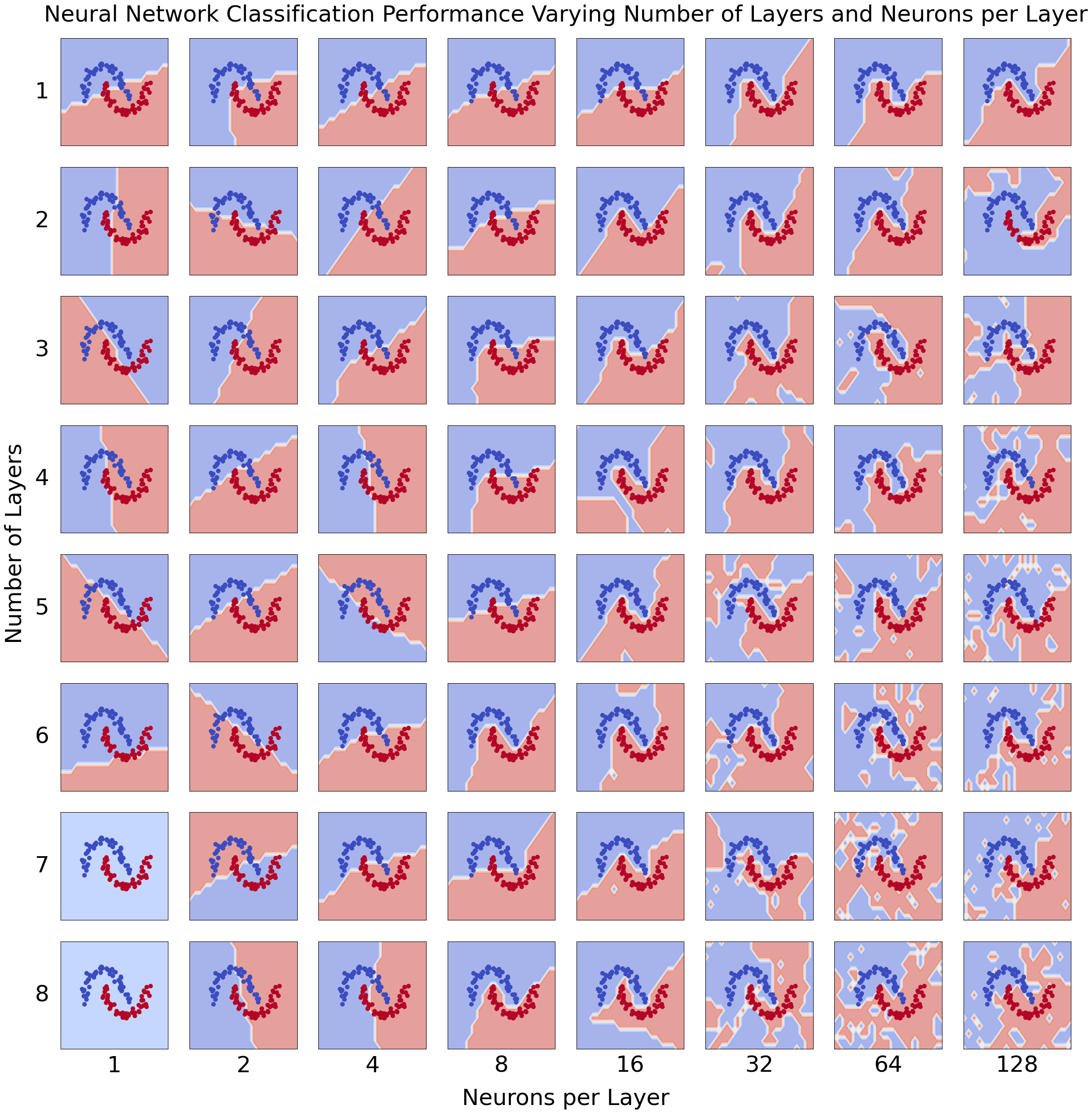
Effects of different sizes
To extend the results of Micrograd's boundary prediction, I repeated the problem a number of times, varying the number of layers in the network and the number of neurons per layer. When the number of layers or neurons per layer is too low, the prediction is too simple for the distribution of data. When it is too high, the prediction overfits the data and tracks spurious correlations. There is a Goldilocks amount that fits the data while still retaining generalizability.
Project Overview
This implementation mirrors Andrej Karpathy's micrograd: a scalar Value type tracks data, grad, the producing op, and parents. Ops build a DAG and backward() topologically sorts nodes and executes stored local backward closures to accumulate gradients.
Supported Operations
Addition, subtraction, multiplication, division (via power -1), power by scalar, tanh, and exp. Each op defines its local gradient rule and contributes to reverse-mode accumulation.
MLP
A simple MLP is built from Neuron, Layer, and MultiLayerPerceptron classes. Activation uses tanh. Parameters are lists of Value objects, so gradients propagate through the whole network.
Training and Loss
Mean squared error over scalar outputs. Mini-batch selection is optional. After computing loss, call backward(), then update each parameter with SGD like p.data -= lr * p.grad and zero grads.